kdanoblog

Legyen G egy egyszerű gráf. Tudjuk róla, hogy ha e egy tetszőleges nemél (szóval e nem éle a gráfnak), akkor G+e-ben több teljes r-es található, mint G-ben. Vagyis e-t hozzávéve a gráfhoz növeljük a K_r részgráfok számát. Még másképp fogalmazva: van r csúcsa G-nek, hogy a köztük vezető élek közül egyedül e hiányzik. Ekkor G-ben legalább C(n,2)-C(n-r+2,2) él található. [Itt a C(n,k) jelölést kényszerűségből használom az "n alatt a k" szám jelölésére, a blog.hu ugyanis – érthetetlen okokból – nem támogatja a TeX-et.]

Gráfok ilyen típusú tulajdonságát telítettségnek hívják (vagyis inkább saturation property-nek, magyarul még nem találkoztam vele, de ez tűnik a megfelelő fordításnak), azaz amikor tetszőleges él hozzáadása valamiféle struktúrát – jelen esetben egy új teljes részgráfot – kényszerít ki. Jellemzően a legkevesebb élt tartalmazó példákat keressük, ami pont az ellentéte a Turán-féle extremális gráfelméletnek. Mint annyi minden, ez a kérdéskör is Erdős (és bandája) munkásságából ered. Konkrétan az első bekezdésben szereplő állítást (tételt) Erdős, Hajnal és Moon bizonyította először, 1964-ben.

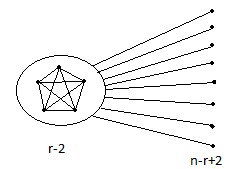
Ennyi élt tartalmazó, és a tulajdonsággal rendelkező gráfot találni egyébként nem nehéz: egyszerűen fogjunk r-2 csúcsot, és kössük össze őket egymással, meg minden más csúccsal is. Szóval pontosan a maradék n-r+2 pont közt menő élek hiányoznak, és persze ha beveszünk egyet, akkor létrehozunk egy K_r-t, az előbbi r-2 csúcs segítségével.

Bizonyítani már nem könnyű, viszont többféleképp is lehet. A kedvencem Bollobás bizonyítása, amely a Bollobás-egyenlőtlenséget használja: Ha adott az A₁, A₂,... A_m valamint B₁, B₂,... B_m halmazrendszer úgy, hogy minden A_i mérete k, minden B_i mérete l, továbbá A_i és B_j akkor és csak akkor diszjunkt, ha i=j, akkor m<=C(k+l,k). Azaz nem tudunk nagyon sok ilyen (A_i,B_i) diszjunkt halmazpárt kiválasztani úgy, hogy a többi közülük alkotott pár ne legyen diszjunkt. Egy kicsit bonyolultnak tűnik az állítás, de egy könnyű példa segíthet elképzelni a dolgot: fogjunk egy k+l-elemű halmazt, az A_i halmaznak válasszunk egy tetszőleges k elemű részhalmazt, a Bi-nek pedig a maradék l elemet. Ez mindjárt mutatja is, hogy k+l alatt k halmzpár elérhető.

Ezt alkalmazva a telítettségi tétel bizonyítása a következő. Minden hiányzó élhez definiálunk egy halmazpárt. A_i lesz az adott él két végpontja, míg B_i a létrehozott K_r-en kívüli összes (n-r) csúcs. Ekkor persze A_i és B_i diszjunkt, és könnyen ellenőrizhető, hogy a többi párnak van közös eleme. Minden A halmaz kételemű és minden B halmaz n-r elemű, tehát alkalmazhatjuk az egyenlőtlenséget: a halmazpárok, azaz a hiányzó élek száma legfeljebb C(n-r+2,2). És ezt akartuk bizonyítani.

Egyébként a Bollobás-egyenlőtlenségnek is több bizonyítása van, közülük a kedvencem Lovásztól származik, és külső hatványokat használ. A k-adik külső hatványa egy V vektortérnek egy másik vektortér, Λ^kV, amelyet V-beli vektorok ún. ék-, vagy külső szorzata generál, mégpedig a k vektorból álló szorzatok. Az ékszorzatnak megvan az a különösen hasznos tulajdonsága, hogy az értéke pontosan akkor nem nulla, ha a szorzatban szereplő vektorok lineárisan függetlenek. Szintén fontos, hogy ha V n-dimenziós, akkor a k-adik külső hatványa C(n,k)-dimenziós. A bizonyítás menete tehát az, hogy V-nek egy k+l-dimenziós vektorteret választunk, és ennek a k-adik külső hatványában megfeleltetünk az A_i-knek lineárisan független vektorokat. Tehát találtunk m lineárisan független vektort egy C(k+l,k)-dimenziós térben, amiből következik az állítás.

Szóval ez az alapprobléma. Rengeteg variációja létezik, megkérdezhetjük például ugyanezt páros gráfokon: Tegyük fel, hogy van egy G=(A,B;E) páros gráfunk, ahol mondjuk |A|=|B|=n, és minden hiányzó A-B közti él behúzásával létrehozunk egy új K_s,t-t , azaz egy teljes páros gráfot, amelynek s csúcsa van A-ban és t csúcsa B-ben. Legalább hány éle van G-nek? A válasz itt is ismert, szintén több bizonyítása van. Először Bollobás bizonyította be: n²-(n-s+1)(n-t+1)-nél kevesebb él nem elég.

Na de mi történik akkor, ha nem kötjük ki, hogy az s csúcs A-ban legyen, a t csúcs pedig B-ben, hanem különböző élekhez különbözőképp állhat az a bizonyos létrehozott K_s,t? Na ez az, amin egy ideje gondolkozunk. Azt tudjuk, hogy az előbbi n(s+t-2)-(s-1)(t-1) élnél kevesebb is elég, de nem sokkal. Sőt, azt Wenying be is bizonyította, hogy legfeljebb egy n-től nem függő konstanssal kevesebb n(s+t-2)-nél a minimális élszám. Sokkal többet viszont egyelőre nem tudunk. Ha sikerül valami eredményt elérnünk, írni fogok róla.