Már elég régóta tervezgetem, hogy ha már ott voltam a CEOI-n, és a feladatok kidolgozásában is szerepem volt, írok egy kicsit róluk. Szóval ebben a posztban megoldásvázlatok, háttérinformációk és megjegyzések várhatóak. Mondjuk mialatt én ezt tervezgettem, megoldásvázlatok szépen ki is kerültek a honlapra (angolul). Ráadásul ez még annál is vázlatosabb, viszont így is elég hosszú poszt lett.. azért talán így is hasznára válik valakinek, ha másnak nem, hát nekem. Na de kezdjük is az elején.
1. feladat (jobs)
Ez a verseny legkönnyebb feladata volt, én ezt a nehézségi kategóriát „ránézésre-feladatoknak” hívom, mert szerintem elsőre is elég nyilvánvaló, hogy mit kell csinálni. Ezek után igencsak meglepődtem, hogy a nyolcfős magyar csapat mindössze három megoldást produkált (az összes versenyző valamivel több mint fele oldotta meg). A feladat a következő:
A mi kis vállalatunknak M munkát el kell végeznie, amikhez gépeket vehet igénybe. Egy gép egy munkával egy nap alatt végez. Tudjuk mindegyik munkáról, hogy melyik nap igénylik. A cél minél kevesebb géppel elérni, hogy minden munka az igényléstől számított D napon belül elkészüljön. A programnak meg kell adnia a minimális gépszámot, illetve hogy ezekkel a gépekkel melyik nap milyen munkákkal végzünk.
Ilyen feladatoknál az első dolog, ami az ember eszébe jut, hogy vajon ha tudom a minimális gépszámot, akkor le tudom-e szimulálni a munkavégzést. És igen, méghozzá lineáris időben. Ennek leprogramozása egy kis odafigyelést igényel, de maga az ötlet eléggé magától értetődik: mohón megpróbálunk elvégezni annyi munkát, amennyit csak tudunk, amit meg nem sikerült, azt visszük tovább másnapra. És akkor máris van egy megoldás: minden gépszámra leszimuláljuk, és kikeressük a minimális mennyiséget, amire el is végzik a munkákat. Ez persze lassú, ha mindent kipróbálunk, de akkor jön a másik rutin észrevétel: ha K gép elég, akkor K-nál több gép is. Tehát alkalmazhatunk bináris keresést, és már kész is az optimális algoritmusunk.
Ezzel a feladattal az volt a galiba, hogy mint azt korábban már említettem, utolsó éjjel vettem észre, hogy a naiv algoritmus is maxpontot ér. Ráadásul nem is egyszerű olyan tesztet csinálni, amire a naiv lassú (lényegében 2-3 napba kell belezsúfolni az össze munkát). De azért sikerült, úgyhogy az 50 pontra volt csak jó a végén.
2. feladat (race)
Nekem a második feladat a race, bár ez a honlapon valami rejtélyes okból megcserélődött (az eredménytáblázatban viszont nem). Itt a mese az, hogy kör alakú tó partján N kikötő található, és mindegyikre meg van mondva, hogy onnan mely más kikötőkbe lehet eljutni. Az eredeti feladat az volt, hogy a hajóversenyünknek a lehető leghosszabb (megengedett) pályát jelöljük ki, amely nem metszi önmagát (egy kikötőt is legfeljebb egyszer érint). Amikor megláttam, kicsit elkezdtem aggódni, mert kettőből ez már a második ránézésre-feladat: egy eléggé sablonos dinamikus programozási probléma. A megoldás ötlete nagyon egyszerű, minden intervallumra ki kell számolni, hogy a bal illetve jobb végponból indulva mi a leghosszabb út, ami csak intervallumbeli csúcsokat használ (amit a kisebb intervallumok értékeiből viszonylag könnyen meg lehet tenni). A körbeindexelés miatt viszont a megoldás kicsit technikás. Például célszerű félig zárt, félig nyílt intervallumokként tárolni a dolgokat. Mindenesetre a verseny előtt megkockáztattam azt az állítást, hogy az eredeti első két feladatot lesz, aki egy óra alatt megoldja (az ötből). Ebben igazam is lett, körülbelül ötven perc után már volt versenyző 140 ponttal, ami pont ezt jelenti.
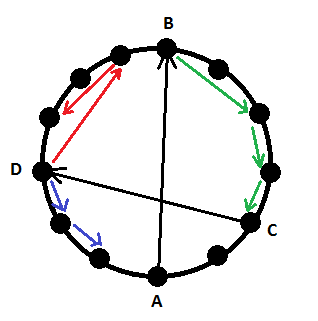
Ugyanis a végleges feladatnak ez csak részfeladata volt, mégpedig 40 pontot érő. A maradék 60 pont az általam javasolt variációra járt (amelyre egyébként nagyon büszke vagyok :) ), amit most nem a megoldó, hanem a kitaláló szemszögéből mondok el, minthogy ebben az esetben ez az én nézőpontom. Szóval az eredetit túl könnyűnek találtam, de hogyan bonyolítsuk? Hát engedélyezzünk metszést. Persze akármennyit nem engedhetünk, mert az egy gráfban keresendő leghosszabb úttá redukálja a feladatot, ami NP-nehéz (sőt teljes), engedélyezzünk inkább csak egyet. Na de akkor ezt hogy oldjuk meg? Kis gondolkozás után semmi más fogódzót nem találtam, mint magát a metszéspontot. Annak négy szabadságfoka van (bár ezt a szót nem szeretem), szóval az két szakasz metszéspontja, azaz négy csúccsal lehet leírni: O(N^4) lehetséges metszéspont van. Ha ez a két szakasz mondjuk AB és CD (ld. ábra), akkor kell még hozzá keresni valami monoton utat B-ből C-be (a maximális ilyet megintcsak dinamikusan könnyű megtalálni), meg még valami nem metszőt A elé és D után. Ezt meg lehet csinálni, bár A és D közé kéne valami határt húzni, kicsit randomkodós, O(N^5)-es algoritmus, nem is tudom, lehet-e jobbat. Node: mi lenne, ha kikötnénk, hogy A-nál kezdődik a pálya. Máris sokkal egyszerűbb, nem négyféle lehet, hanem csak kétféle, O(N^4)-es algoritmus magától értetődik. Lehet-e jobbat? Lehet! Azt kell észrevenni, hogy ha a D-ből az A felé kunkorodik a pálya, akkor minél messzebb van az A a D-től, annál több hely van kibontakozni, annál hosszabb befejezés lehetséges. Szóval ha B-t C-t és D-t rögzítjük, akkor az A-t a C-hez lehető legközelebbinek kell választani. Ezzel – és mindenféle előszámolgatással – O(N^3)-ös algoritmus is megvalósítható.
A pontozás volt még egy vicces téma, két dolog ugyanis üti egymást: szelektálhatunk feladatbonyolultság-alapon, meg futásidő alapján. Tudniillik arra is akartunk részpontszámot adni, ha valaki csak a kereszteződésmentes megoldást kódolja le, amire ugyebár köbös az algoritmus, viszont arra még többet akartunk, ha valaki a kereszteződősre is tud egy N^4-eset (ez ugyanis szerintem nehezebb, mint a kereszteződésmentes). A dilemmát az okozza, hogy ha valaki megír egy N^4-es algoritmust, az könyen kifuthat az időből a kereszteződésmentes esetben is, holott arra tudna köböset is, vagyis a jobb megoldással pontokat vesztene néhány teszteseten. Ezt elkerülendő egyetlen járható út jutott eszembe: előre rögzítjük, hogy kereszteződéses vagy kereszteződésmentes megoldást keresünk-e. A kereszteződésmentest megoldó program, ahogy már említettem, 40 pontot ért. Kis kellemetlenség az is, hogy (könnyen láthatóan) a kereszteződéses megoldás legfeljebb eggyel hosszabb a kereszteződésmentesnél, de ezt elég jól ki lehet küszöbölni azzal, hogy a pálya kezdőpontját is kiíratjuk. Az én első mintaprogramom egyébként elég lassú volt, a technikai dolgokat ugyanis nem optimálisan hajtottam végre, és a sok mod n számolás több mint megkétszerezte a futásidőt. NGG programjának adattárolását használva azonban ki tudtam optimalizálni, és az ez alapján belőtt időlimit 70-75 pontot engedett az N^4-es megoldásnak, az optimálisnak pedig természetesen 100-at.
3. feladat (circuit)
Ez a feladat eredetileg más volt. Kicsit nehezebb, de valamivel rondább is. Végül egy egyszerű zárt poligonnak kellett megadni az origóból látszó csúcsait. N logN-es megoldást találni rá nem nehéz, inkább a kódolás az időigényes, és könnyen bele is lehet zavarodni. Az ötlet mindössze annyi, hogy szög szerint rendezzük a csúcsokat, és végigmegyünk rajtuk. Mindig lesz egy origóhoz legközelebbi szakaszunk, ami vagy kitakarja a soron következő csúcsot, vagy nem. Ha kitakarja, akkor elfelejtjük a csúcsot, ha nem, akkor bevesszük a kiírandók közé, és lesz egy új aktuális szakaszunk. Szöszmötölés, de működik.
Viszont meg lehet ezt csinálni lineárisan is: első körben itt megkeressük a legkisebb szögben látszódó csúcsot (origóból nézve az x-tengellyel bezárt szög), majd onnan indulva körbejárjuk a poligont. Érdekes módon nem mindegy, hogy merre indulunk, legalábbis az én megoldásom csak az origóhoz közelebbi szakaszról indulva (óramutató járásával megegyező irányban) működik. Ebben az esetben ugyanis – és ez az észrevétel a megoldás kulcsa – tárolhatjuk a kiírandó csúcsokat egy veremben. Mert mi történhet? Amíg növekszik az origóból a szög (és tudom, hogy jó lenne egy ábra, de most arra nincs időm), addig semmi probléma, szépen rátesszük a verem tetejére a következő csúcsot. De mi van, ha visszafordul? Hát attól függ. Ha jobbra fordul, azaz elbújik az eddigi szakaszok mögé, akkor nem is érdekel minket, hogy mit csinál amíg ki nem bújik. Ha viszont balra fordul, akkor a verem tetejéről néhány csúcsot ki fog takarni. Na, ezeket mind kiszedhetjük (azt a felső csúcsot is, amit az eddigi szakaszok nem takarnak ki, ugyanis a poligon előbb-utóbb azt megkerülve fog visszajutni a kiindulópontba). És igazából még van két eset, amiket stalactite és stalagmite case-nek neveztem el (ez a magyarban kevésbé működik, mert a geológusokon kívül kb. mindenki cseppkőnek hívja függő- és az állócsepkövet is), és nevéhez illően vagy egy fölülről lelógó izé mögé bújhat el a következő csúcs, vagy egy alulról fellógó izé mögé. Viszont ezeket az eseteket is lehet konstans időben kezelni, és ebből egy valóban lineáris algoritmus jön össze. Egyébként a stalagmite-esetet eredetileg nem vettem észre, és erősen meglepődtem, amikor megláttam, hogy a programom 95 pontot ért. Aztán megtaláltam a hibát, és most remélhetőleg jó.
4. feladat (highway)
Az a bizonyos. (Már írtam a felmerült problémákról ennél a feladatnál.) A feladat szövege szerint kézpeletbeli országunkban van néhány városunk, és autópályát akarunk építeni. Csodák csodájára a városok lefedhetők két egyenessel. Csak épp mi nem tudjuk, hogy melyik ez a két egyenes, a feladatunk ezt meghatározni. Mégpedig csak olyan kérdéseket tehetünk fel, hogy három város egy egyenesre esik-e. Az egyenes meghatározásához két-két várost kell megadnunk rajtuk.
Ez első olvasásra geometriafeladatnak tűnhet, de valójában nem az: lényegében két diszjunkt halmazunk van, és egy kérdés során három elemről eldönthetjük, hogy ugyanabba a halmazba esnek-e. Azt igazából én javasoltam ehhez, hogy a mesének megfelelően ha nem három különböző városra kérdeznek rá, akkor mindenképp igen legyen a válasz (ugyanis legfeljebb két város mindig egy egyenesre esik). Hatékony megoldást egyáltalán nem nehéz adni rá, mégpedig olyat, amely legfeljebb N/2+1 kérdésből biztosan megadja az egyeneseket, és sokkal kevesebből bizonyíthatóan nem is lehet megoldani (a cél a minél kevesebb kérdés alkalmazása volt). Mármint ez akkor egész egyszerű, ha nem kell speciális esetekkel vacakolni, de pont azért javasoltam a feladat utolsó mondatát (felteheted, hogy N/3 kérdést ki fog kényszeríteni a program), valamint hogy N mindig legalább 40, hogy ne kelljen olyasmivel vacakolni, amikor több mint egyszer kap nem választ a program. Ugyanis ha az ilyen – konstant lépésben kezelhető, de kellemetlen és kis N-re bezavaró – helyzeteket kizárjuk, akkor a válaszolóprogramnak érdemes igeneket válaszolni.
Sok megoldás van, nagyon vázlatosan az enyém azt csinálta, hogy sorra kérdezi az (1,2,3)-at, (3,4,5)-öt, stb amíg „igen”-t kap, míg ha (k-2,k-1,k)-ra „nem” a válasz, akkor (k+1,k+2,k+3), (k+3,k+4,k+5), stb. a következő „nem”-ig. Ha összejön a két nem, abból 3 kérdéssel megtalálható a két egyenes, ha viszont nem akkor a maradékkal lehet kicsit szöszmötölni, és úgy is gyorsan találunk megoldást. A vicces a dologban az, hogy erre jó válaszológépet nehéz írni (nem is tudom, hogy kell), vagyis olyat, amely minél több kérdésre kényszerít. Ja, és gyors. Mert a versenyen használt verzió elég naiv volt: addig mondta az igeneket, amíg csak lehetett, és ez azért nem optimális. Próbáltam kicsit javítani rajta, de nagyon bonyolult lett, és időm sem volt rá, úgyhogy maradt a régi.
5. feladat (wagons)
Néhány vagonnyi szemét várakozik a vágányon arra, hogy feldolgozzuk őket, mindegyiknek tudjuk a típusát. Minden napra beállíthatjuk a feldolgozóüzemet, hogy milyen típusokat tud aznap feldolgozni, de csak néhány ilyen séma közül választhatunk. Felhasználhatunk még egy segédvágányt, ami veremként funkcionál, azaz ha a soron következő vagont nem akarjuk feldolgozni, félrerakhatjuk a segédvágányra. És akkor következő nap megint megpróbálhatjuk feldolgozni, legkorábban a legutóbb odakerülteket. A feladat megmondani, milyen sémákat használjunk, ha három nap alatt a lehető legtöbb vagont akarunk feldolgozni, és végül a segédvágánynak üresen kell állni. Fontos információ, hogy minden típus legfeljebb 10 sémában szerepel, ezt használja ki a hivatalos megoldás is.
Szerintem ez volt a legnehezebb feladat, egyben az egyetlen, amit nem tudtam megoldani. Mondjuk először könnyebbnek tűnt, mert azt hittem, a segédvágányról vissza is lehet mozdítani vagont, pedig nem. Az első észrevétel (ami nélkül esélytelen hozzákezdeni a megoldáshoz), hogy ha fel tudjuk dolgozni az első néhány vagont, akkor azok három szakaszra bonthatóak [AC][AB][BC] módon, ahol A az első nap használt séma, B a második és C a harmadik naphoz tartozó, és ahol [AC] alatt azt értem, hogy az első néhány vagon mindegyike beleesik az A vagy C sémába, a következő néhány az A-ba vagy B-be, aztán a maradék a B-be vagy C-be. Egy ötlet lenne, hogy mohón próbáljuk megtalálni a szakaszhatárokat, de ez nem jó. Sajnos egy hasonlóan naiv megoldás mégis maxpontot ért, nem tudom, hogy a 100-pontos megoldások közül hányan alkalmazták azt.. Az én ötletem olyasmi volt, hogy bináris keresésekkel próbáljuk megtalálni a szakaszhatárokat, de borzasztó bonyolult lett, és valszeg el is kódoltam, mert nem sok pontot szerzett.
A hivatalos megoldás ezzel szemben egy véges automatát készített, amitől nem kell megijedni, csak annyit jelent, hogy állapotai vannak, és az aktuális állapot alapján fut az algoritmus, esetleg lép át másik állapotba. (Mondjuk kicsit fura, hogy HGyula ezt a feladatot választotta, ugyanis az IOI-syllabusban explicite ki vannak zárva az automatás feladatok, márpedig őt az ilyesmi zavarni szokta. De engem nem zavar, tőlem jöhetnének folyamok és mátrixhatványozósan lineáris rekurziót megoldó algoritmusok is.) Szóval állapotok kellenek, amik nyilván azt fogják meghatározni, hogy: (1) melyik szakaszban vagyunk épp, (2) A, B és C közül melyik van már fixálva. Ez egy nemdeterminisztikus automata lesz, ami csak annyit jelent, hogy a futás szétágazhat, azaz több esetre bomlik. Egész pontosan azért, mert amikor épp az i-edik vagonnál tartunk, és fixálni akarjuk B-t, hogy az feldolgozza az illető vagont, akkor itt van (legfeljebb) 10 lehetőségünk, és bizony mindet meg kell nézni. De szerencsénk van, mert csak három sémát kell rögzítenünk, így legfeljebb háromszor ágazik 10-felé az automatánk, vagyis összesen 1000-féle futás lehetséges (illetve kicsit több, mert még az állapotoknál is van némi szabadságunk). Ha pedig ezt valaki megérti, és csinál belőle algoritmust, az olyan 10^3 * N nagyságrendű lépésben le is fog futni.
6. feladat (network)
Eredetileg az volt a feladat, hogy adott egy irányított gráf, amiben egy csúcsból a másoikba legfeljebb egy út vezet, továbbá a gyökérből minden más elérhető, és meg kellett adni a minimális számú újonnan behúzandó irányított élt, hogy bármely pontból bármely másikba pontosan egy út vezessen. Már az is érdekes, hogy ilyen létezik egyáltalán, bár ezzel nem kellett foglalkozni a versenyen. Ez volt a negyedik feladat, ami viszonylag könnyűnek tűnt nekem, bár tény, hogy azért némi gondolkodást igényel. Nehezíteni viszont nem lehet, úgyhogy egy (kicsit unalmas, de mégis pluszmunka) mellékfeladattal kiegészült. Azzal most inkább nem is foglalkoznék.
Igazából ha az ember rajzol egy megfelelő input gráfot, akkor elég egyértelmű, hogy hogy kell behúzogatni az éleket. Valóban, majdnem egyértelműen meg vannak határozva. Igazából kicsit jobban látszik a dolog, ha a gráfunkban nincs (irányított) kör, azaz egy fenyő. Ekkor úgy kell behúzni az éleket, hogy ha van egy elágazás, oda egy kivételével minden leszármazottól be fognak futni az élek, az a maradék egy pedig megpróbál keresni magának egy gyökérhez közelebbi elágazást. Ennek megoldására egy lehetséges mód, hogy mélységi keresést csinálunk, és ha eljutunk egy levélhez, berakjuk az „innen még megy ki él” vermünkbe. Majd amikor visszalépünk egy elágazáshoz, és új irányba indulunk, akkor kivesszük a verem tetején szereplő csúcsot, és onnan élt húzunk az elágazásba. Ez az algoritmus lényegében működik akkor is, ha vannak körök, csak kicsit tágabban kell értelmezni a levél, és kicsit szűkebben az elágazás fogalmát: lényegében ki kell törölni az erősen összefüggő komponenseket, és a maradék gráfban kell megoldani a feladatot. Ehhez mondjuk nem kell ténylegesen megkeresni az erősen összefüggő komponenseket, ugyanis ilyen típusú irányított gráfban (nincs keresztél!) egész egyszerűen megállapítható, hogy az aktuális csúcsunk egy gyereke felé vezető él benne van-e irányított körben (mégpedig az irányítatlan gráfok kétszeresen összefüggő komponenseinek megkereséséhez használt módszerekkel). Viszonylag kis maszatolással, de viszonylag nagy odafigyeléssel összerakható ebből egy lineáris algoritmus. (Egy mélységi keresés az egész. Pontosabban a másik részfeladattal együtt kettőre is szükség van.)
